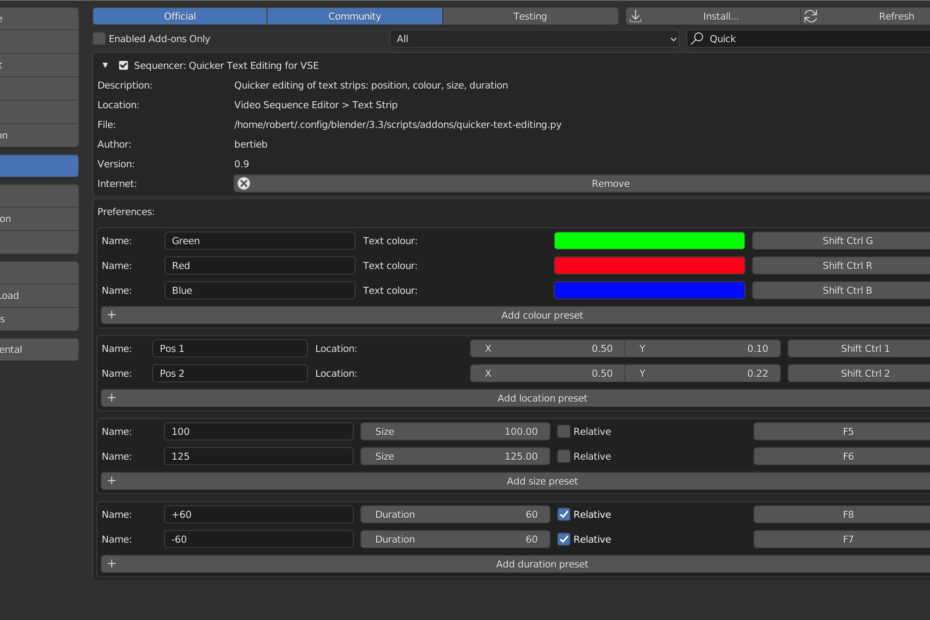
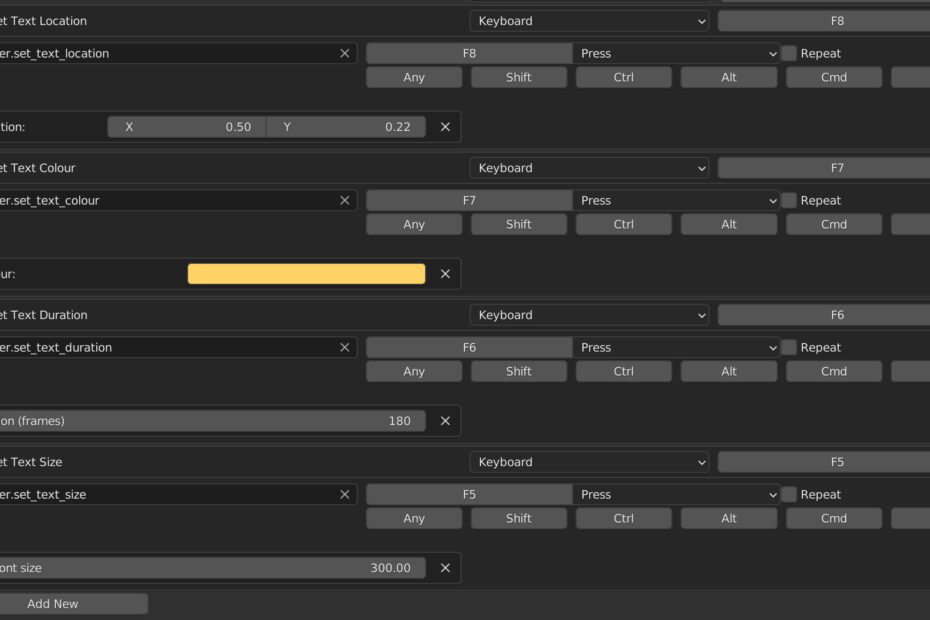
Quicker Text Editing in Blender (Part 13): CollectionProperty, KeyMapItem ID, Preferences Pitfalls
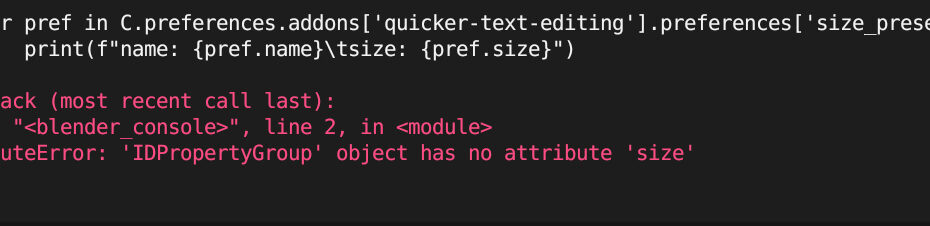
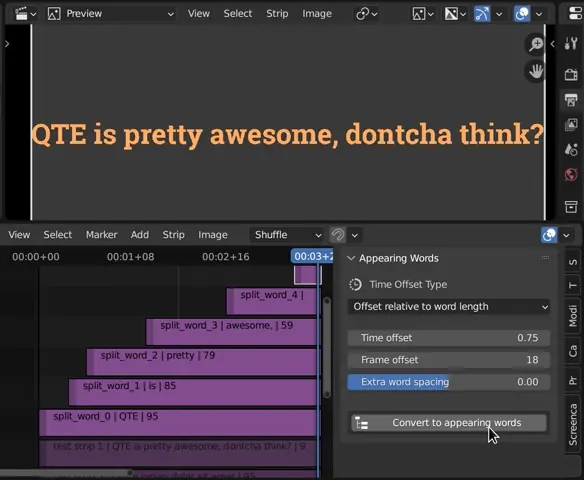
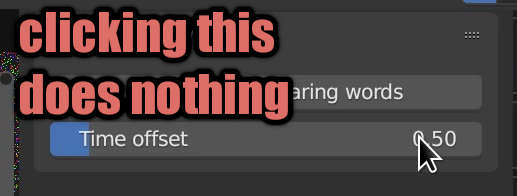
There were many pits and I fell in them all Background Context In part 12 I mentioned the issue with storing operator properties in a… Read More »Quicker Text Editing in Blender (Part 13): CollectionProperty, KeyMapItem ID, Preferences Pitfalls